 A raíz de una duda que me surgió en el último artículo del Sr. Chulilla me puse a buscar cuanto medía de ancho y alto la pantalla del Surface Pro 3. Ojo, no cuanto mide de ancho y alto el Surface Pro 3 pues eso está publicado mil veces, no, solo cuanto mide la pantalla. Aquí les explico como se calcula.
A raíz de una duda que me surgió en el último artículo del Sr. Chulilla me puse a buscar cuanto medía de ancho y alto la pantalla del Surface Pro 3. Ojo, no cuanto mide de ancho y alto el Surface Pro 3 pues eso está publicado mil veces, no, solo cuanto mide la pantalla. Aquí les explico como se calcula.
Vale, ¿qué sabemos? Sabemos dos cosas, una que la diagonal de la pantalla es de 12″ y dos que su ratio de aspecto es 3:2.
He de decir en honor a Juan Luis Chulilla que también me parece decimonónico que sigamos hablando de las diagonales de las pantallas en las llamadas medidas imperiales, unidades de medida que solo se usan en dos o tres países del mundo y que de imperiales tienen ya lo que yo de funambulista.
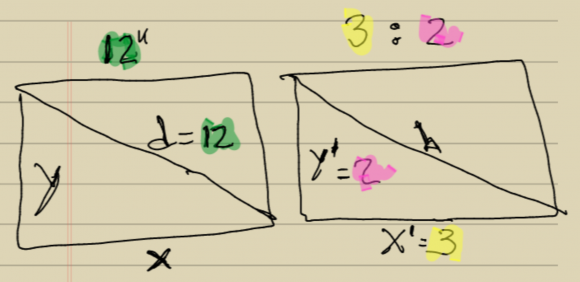
Vale, ¿cómo lo calculamos? Básicamente debemos imaginar que tenemos dos triángulos que son equivalentes. Uno del cual sabemos su hipotenusa y otro del cual sabemos sus catetos.
Para efectos de posibles cálculos de otros casos ver lo que está marcado en verde, es la diagonal que conocemos, esto es 12″. Y en amarillo y rosa está marcado el ratio de aspecto 3:2. Simplemente sustituyendo esos valores por los nuestros podemos aplicar nuestros propios cálculos, por ejemplo, una pantalla de 10″ con ratio 16:9 Pues pondríamos 10 en el verde, 16 en el amarillo y 9 en el rosa.
Bueno calculamos primero la diagonal que no conocemos. La del triangulo de la derecha del dibujo que puse antes usando el Teorema de Pitágoras que dice que la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos. O sea en este caso:
He marcado el valor de h en azul pues en caso de otras medidas ese valor se usará en siguientes cálculos y es para que lo sustituyáis fácilmente. Como vemos la diagonal del triangulo de la derecha mide 3,605 pulgadas.
Vale ahora como tenemos dos triángulos equivalentes podemos hacer una regla de tres. Si h es equivalente a d entonces X’ es equivalente a X de modo que X es igual a X’ por d dividido entre h:
Si aplicamos nuestros valores a esa fórmula tendremos:
De modo que ya sabemos que nuestro ancho (X) del monitor son 9,98 pulgadas. Ahora lo pasamos a centímetros para dejar de usar unidades de siglos pasados sabiendo que cada pulgada son 2,54 centímetros, así tenemos:
Nuestro monitor por tanto mide 25,36 centímetros de ancho. Ahora para calcular el alto otra vez usamos una regla de tres multiplicando por (en este caso) 2 y dividiendo por 3 (el ratio era 3:2, ¿recuerdan?):
Y ya sabemos que el alto es de 16,91 centímetros.
Por tanto una pantalla de 12 pulgadas con ratio 3:2 mide 25,36 centímetros de ancho y 16,91 centímetros de alto.
Podemos repetir los cálculos como digo cambiando la diagonal y los valores de ratio de aspecto.
Fácil, útil y muy off-topic. ¿No?
Os dejo mis cálculos completos tal y como los escribí en mi Dell Venue 11 Pro de 10,8″ y el programa S-Note:


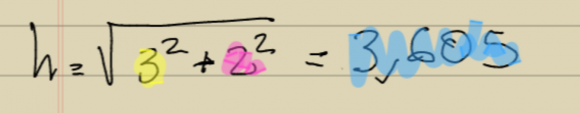
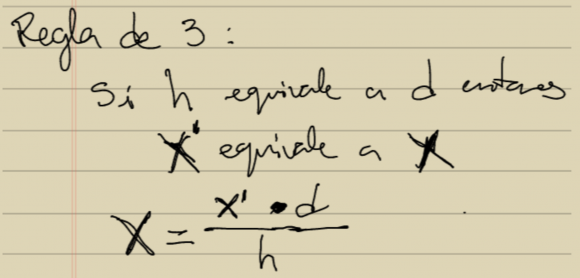
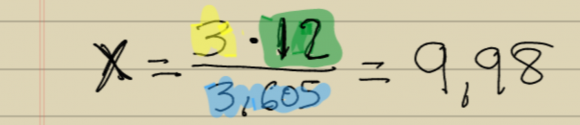
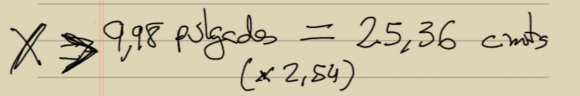
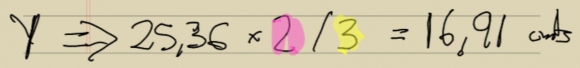




Síguenos